MATLAB PHYSICS MyCourses

Matlab解物理问题的常用算法

MATLAB Essentials 4

Posted by Yuxuan Zhang on December 17, 2019

Index of Matlab Essentials

数值微分

离散数据微分的计算方式

  1. 前差:
    𝑓'(x) = (𝑓(𝑥 + h) − 𝑓(𝑥))/h
  2. 后差:
    𝑓'(x) = (𝑓(𝑥) − 𝑓(𝑥 - h))/h
  3. 均值:
    𝑓'(x) = (𝑓(𝑥 + h) − 𝑓(𝑥 - h))/2h

常用微分运算命令

命令 描述
dX = diff(F [,n [,dim ]]) 对维度为 dim 的矩阵(向量) X 作 n 阶差分 (仅作差, 需手动点除步长)
[dX [,dY]] = gradient(F, h) 当输入 F 为向量(一维)时, 返回 F 的导数 dX
当输入 F 为矩阵(二维)时, 返回 F 分别在 x 和 y 方向上的梯度 dX dY
标量 h 定义相邻元素的步长
del2(F, h) 用法同 gradient() 但是返回的是拉普拉斯算符的运算结果

Matlab求方程零点

求单调函数实根的算法

1. 对分法(二分查找法)

基于定理:

若单调连续实函数 f(x) 满足 f(a)*f(b) < 0, a<b 则 f(x) 在 (a,b) 区间存在实根.

只要找到一组 a, b 使得 f(a)*f(b) < 0, 就可以连续使用二分法迭代 a 和 b 的值, 直到 a-b 足够小(小于设定的下限).

特点: 稳定, 速度较慢

2. 切线法(牛顿迭代法)

基于 Taylor Series:

当 x -> xn 时, f(x) ~ f(xn) + f’(xn) * (x - xn)

因此, 对于一组 a, b 使得 f(a)*f(b) < 0 , 可以用上述 一阶泰勒展开函数的零点 代替二分法作为迭代的基准点.

特点: 速度较快, 但是对于不同初始条件, 其行为难以预测

3. 弦割法

将对分法直接求中点改为考虑 f(a), f(b) 作为权重的加权平均.

特点: 方法 1 的改进版

4. 迭代法

将函数写成零点方程, 并化成 x = f(x) 的形式, 产生迭代公式: x_k+1 = =f(x_k).

这种方法需要手工验证迭代公式在零点附近收敛, 并且需要针对每一个不同的函数表达式手工转换, 因此不常用.

求单调函数实根的命令

命令 特点
fzero() 解 非刚性 问题
roots() 只适用于多项式求根, 可以求出所有根, 包括虚根
fsolve() 适用于任意自定义函数, 需要自定义试探点集, 返回的根数量不多于输入的试探点数量

fzero()

x = fzero(F, x0);
x = fzero(F, x0, options, p1, p2, ...);
[x, fval] = fzero(...);

fzero() 的输入变量 F 必须是单变量函数的句柄,

x0可以是标量(scalar), 表示开始搜索的 x 值; 也可以是 1*2 的向量(vector), 表示进行搜索的范围.

注意: fzero 只返回它找到的第一个零点, 对于多零点函数, 无法找到给定范围内的全部根.

roots()

x = fzero(C);
% For example:
% C = [a,b,c,d,e,f]
% means equation:
% a*x^5 + b*x^4 + c*x^3 + d*x^2 + e*x + f = 0

输入变量 C 是一个 1*n 向量, 其中的元素代表多项式方程各幂次项系数, 由高次项到低次项排列.

输出 x 是一个向量, 包含方程的所有根(包括虚根).

fsolve()

[X,FVAL] = fsolve(FUN, X0, ...);
% FUN is a customed 1 input function,
% X0 is a vector of all strat points
% X contains all possible solutions,
% if fsolve fails to find a solution from X0(a),
% X(a) will be same as X0(a)

R-K法解微分方程初值问题

R-K方法即 Runge-Kutta Methods ( 龙格—库塔法 ) .

R-K法是一种改进的离散化数值积分算法

由于计算机系统是离散系统, 无法做到绝对的连续积分, 因此必须采用离散化的递推关系式进行数值积分运算. 在离散化运算中, 时间( t 轴)以及空间( y 轴)的不连续性会导致量化误差, 这种误差可能会随积分运算进行累积(在比较好的情况下, 也有可能相互抵消), 对积分结果造成不可接受的误差.

数值求解微分方程最基本的方法是 Euler迭代法:

已知 dy/dt = f(t,y), F(t0) = y0 , 数值化(离散化)步长设为 h

则 Euler迭代法 的递推式为 yi+1 = yi + hf(ti, yi)

使用上述递推式可以一定程度地求出微分方程的数值解.

R-K法是一种改进的, 根据初始条件在一定范围内数值求解微分方程的方法.

R-K法的思想就是通过预测下一步的落点, 计算两步之间 n 个点的 加权 平均斜率, 取代原先粗糙的斜率预测值, 从而减小步长范围内 f(t,y) 的变化导致的离散化误差.

N 阶R-K法的加权平均需要用到 N 个系数, 这些系数可以手工选取, 应当保证归一化(和为一).

变步长R-K法 - 兼顾精度和速度

定义 当前步长误差 为 E0 = y(Euler) - y(R-K,h) , 减半步长误差 为 E1 = y(R-K,h) - y(R-K,h/2).

通过比较 E0 和 E1 的差异(例如,数量级差 1 )来决定是否减半步长. 如果减半步长后和下一级误差相比仍不满足条件, 就继续减半步长, 直到满足条件为止.

这种方法可以保证每一步的误差总是处在可以接受的范围之内, 同时一定程度上保证了解微分方程的效率.

这种逻辑建立在假设 误差随步长的减小单调递减 之上, 但这一假设成立的条件待推导.

ode函数集解初值问题或事件问题

初值问题 是指在给定微分方程和初始条件的情况下求解 原函数 的问题.

事件问题 是指在给定微分方程和初始条件的情况下求指定的状态 何时何地出现 的问题

函数 特点 算法和适用性
ode45() 解 非刚性 问题
精度中等		 使用龙格—库塔法的四、五阶算法
适用于大多数场景
ode23() 解 非刚性 问题
精度低		 使用龙格—库塔法的二、三阶算法
适用于容差较大或适度刚性问题
ode113() 解 非刚性 问题
精度由低到高		 使用Adams-Bashforth-Moulton PECE法
适用于容差要求严格，或者常微分方程函数计算代价较大的情况
ode15s() 解 刚性 问题
精度由低到中等		 使用可变阶次的数值微分(NDFs)算法
适用于ode45计算很慢(由于刚性)或有质量矩阵的情况
ode23s() 解 刚性 问题
精度低		 使用修正的RosenRock算法
适用于对误差要求不高的情况或者有质量矩阵的情况
ode23t() 解 刚性 问题
精度低		 使用自由内插法的梯形法则
适用于要求结果无数值衰减的适度刚性问题
ode23tb() 解 刚性 问题
精度低		 使用TR-BDF2算法
适用于于对误差要求不高的刚性问题或者含有质量矩阵情况

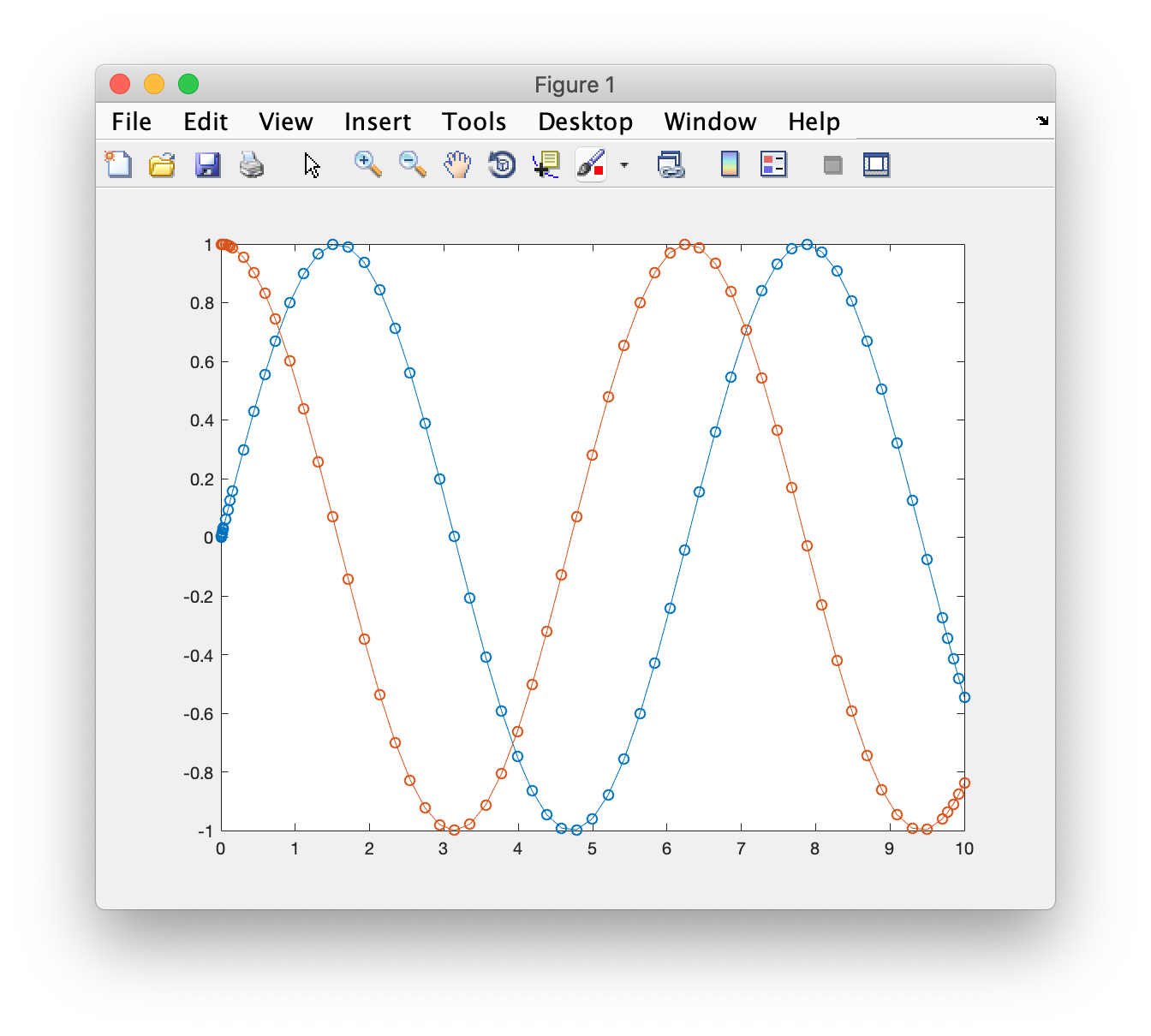
ode 函数解初值问题的用法, 以 ode45() 为例

% USAGE
TSPAN = [T0 TFINAL];
[TOUT,YOUT] = ode45(ODEFUN,TSPAN,Y0);
[TOUT,YOUT] = ode45(ODEFUN,TSPAN,Y0,OPTIONS);
SOL = ode45(ODEFUN,[T0 TFINAL],Y0...);
% Working Example - sin() function solution
>> F=@(t,y)[y(2); -y(1)];
>> ode45(F, [0, 10], [0, 1]);

示例: ode45 解三角函数微分方程

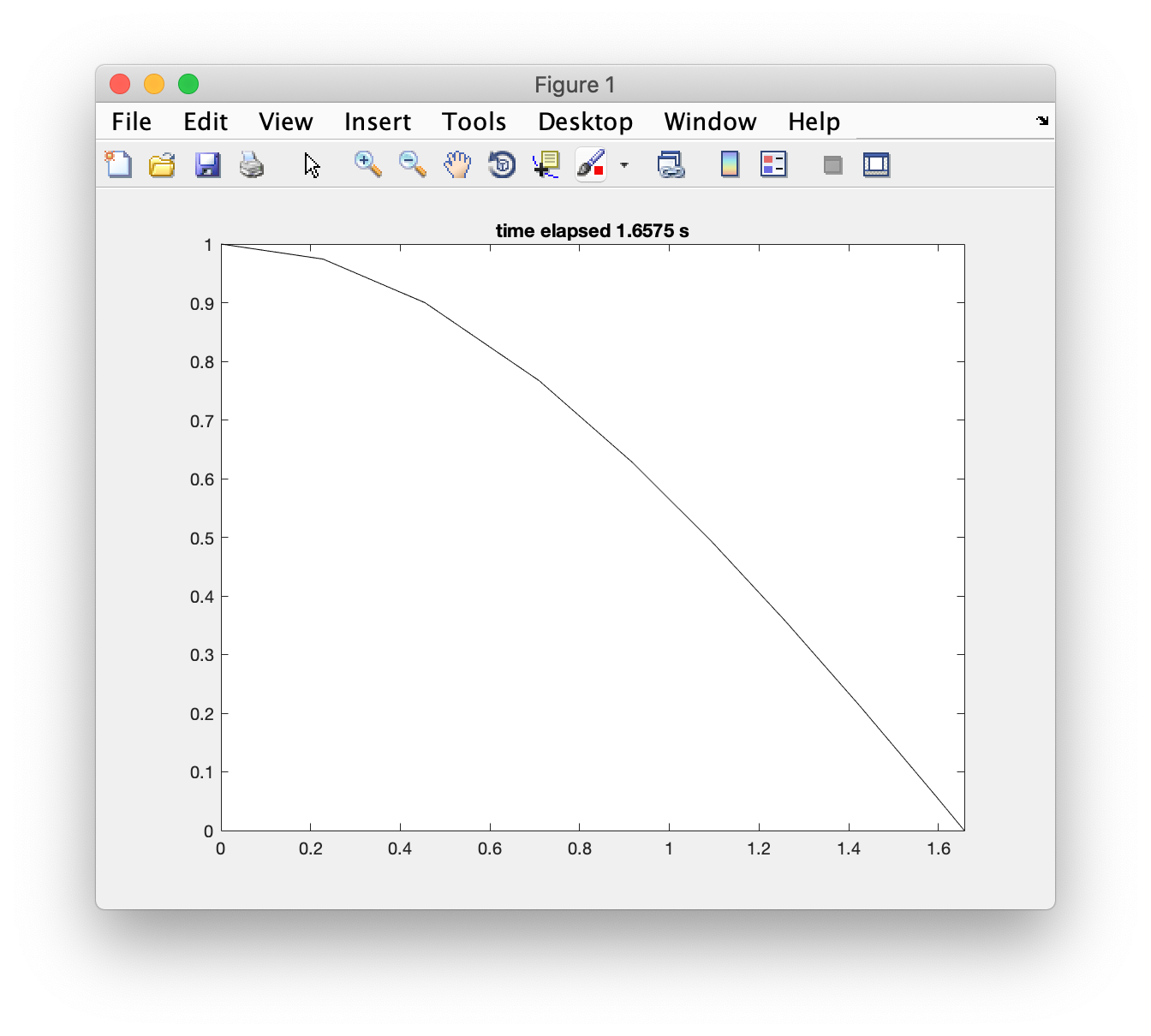
ode 函数解事件问题的解法, 以 ode45() 为例

本例中物理模型为一个下落的物体(考虑空气阻力, F = ma ～ v^2 ), 中止事件为物体触地.

微分方程为 y" = -1 + y'^2

即 f=@(t,y)[y(2); -1+y(2)^2];

% USAGE
% OPTIONS.EVENTS Controls the termination of the intergration.
% set it by calling odeset('event',handle)
[TOUT,YOUT] = ode45(ODEFUN,TSPAN,Y0,OPTIONS);
SOL = ode45(ODEFUN,[T0 TFINAL],Y0...);
% Working Example - sin() function solution
f=@(t,y)[y(2); -1+y(2)^2];
opts=odeset('events',@trigger,'RelTol',1.e-6); %设置触发事件和精度
handles = ode45(f, [0,Inf], [1; 0], opts);
plot(handles.x,handles.y(1,:),'*-k');
title("time elapsed "+handles.xe+" s");
axis([0 handles.xe 0 1]);
function [gstop,isterminal, direction]=trigger(t,y)
  gstop = y(1);
  isterminal = 1;
  direction = -1;
end

示例: ode45 解事件问题

刚性问题

刚性, 指Jacobian矩阵的特征值相差十分悬殊. 也可以定义为函数在某一点附近剧烈变化, 但是在其它位置比较平缓的问题.

边值问题

边值问题可以通过转化为初值问题求解:

  1. 在任一边界上猜测一个边界条件(边界点的导数), 按初值问题解方程

  2. 若所得解不满足另一端的边界条件:

    • 重新猜测一个边界条件重新解方程(打靶法)
    • 或对所得的解加以某些修正(修正法)

pdetools

迭代法解线性方程组

将多项式写成 xk = a1x1 + a2x2 + a3x3 + … 的迭代多项式形式, 给向量 X = [x1,x1,…] 赋随机初值, 并令其按上述迭代关系演化, 在足够长的演化次数后即可得到线性方程组的近似精确解.

这一方法与矩阵的左除类似, 但具有独特的优点.

FEATURED TAGS
Cheatsheet MyCourses MATLAB PHYSICS Courses Jekyll Micro Computer
RELATED SITES